作者:本质教育 魏旭东
本质教育高考数学破题解析开课啦!!!
每周一、三、五更新新篇,将会从18年高考开始,致力于用三招将高考数学中具有代表性的题逐个击破。
本质教育高中数学致力于培养学生的思维方式,提供思维能力,打破固有的刷题和死记硬背模式,让学生冲刺高考数学的140+。
本质教育高中数学网址:本质教育高中数学
数学三招:翻译、特殊化、盯住目标
翻译:我们遇到中文的时候,往往需要把它们“翻译”为数学的语言。大家常 常听到的“数形结合”实际上就是“翻译”的一种,借助于直角坐标,几何可以“翻译”为代数,代数也可以“翻译”为几何。
特殊化:简单来说,就是用具体的简单数字代替变量(更进一步,研究题目前提/该条件的必要条件)。我们一般从最特殊、最极端的例子开始。常用于将抽象难以理解的题目特殊化为具体的例子来帮助我们真正理解题目,理解每一个已知数、条件的作用。我们有时需要借助特殊化的结论,有时则可以利用其方法。
盯住目标:即根据题目,试着联想相关的定理、定义、方法,并运用之,试着把已知,条件(前提)和目标联系起来,不断地通过置换目标来改造题目。任何一道题目都是在已知(前提)和未知(结论)之间构建桥梁,问问自己,我们还有什么已知但没有使用吗?
三招的概念虽然简单易懂,但是如果要熟练运用,难度还是很大的,所以,也就有了我们本质教育高中数学
2018.11.19更新
(过于简单的题目不再赘述,这里我们只选取稍微凸显思考的题)
2018北京卷
试卷第18题
设函数
(1)若曲线在y=f(x)在点(1,f(1))处的切线与X轴平行,求a;
(2)若f(x)在x=2处取得最小值,求a的取值范围。
三招破题
(1)翻译:若曲线在y=f(x)在点(1,f(1))处的切线与X轴平行 此切线斜率为0,即f'(1)=0
所以我们只需要求出f'(1)看一看,
,
所以显然直接根据这个式子我们可以求出
.
(2)翻译:若f(x)在x=2处取得最小值,这句话可以翻译出什么东西来?
首先我们考虑函数的定义域,显然是R,则这里的最小值很可能是这个函数的极小值,那这个点是不是极小值点呢,我们只需要计算f'(2)看看即可。
根据第一问的结论, ,那么,
x=2这个点确实也是极小值点。
那这个题逻辑就清楚了,这个点是极小值点,我们只需要根据在此点左右f'(x)的正负性,让其满足成为最小值点的条件即可,然后它肯定是与a有关的,那么目标自然也就联系上了。
极小值点如何成为最小值点,是不是在这个点的左边,导函数恒小于等于0,函数单调递减,在这个点的右边,导函数恒大于等于0,函数单调递增,即可。
那么我们观察导函数,判断其正负性,显然与 没什么关系,那我们只需要讨论前面部分,
那么,
我们令 ,
一个二次函数,怎么判断其正负性,很显然,而且我们的目标是a,二次项系数也是a,
那自然联想到从a下手,首先讨论它是不是二次函数,
①a=0时,g(x)=-x+2,在x=2左边是大于0的,显然已经不符合刚才我们上面的逻辑讨论了,必须抛弃。
②a 0时,我们是不是二次函数还有两个重要参数
,对称轴为
,
即g(x)至少与x轴有一个交点,对称轴也知道了。
我们接下来要做的是什么,是不是根据刚才的目标,讨论这个函数的正负性啊,那么显然有一种特殊情况,它与x只有一个交点,恒正或恒负,此时不符合题意。
Ⅰ. 时,
,f(x)此时单调递增了,不符合题意。
那么接下来怎么讨论,是不是要满足在这个点的左边,导函数恒小于等于0,函数单调递减,在这个点的右边,导函数恒大于等于0,函数单调递增。
这里笔者给出一张图说明其中一种情况,剩下的同学们自己动手
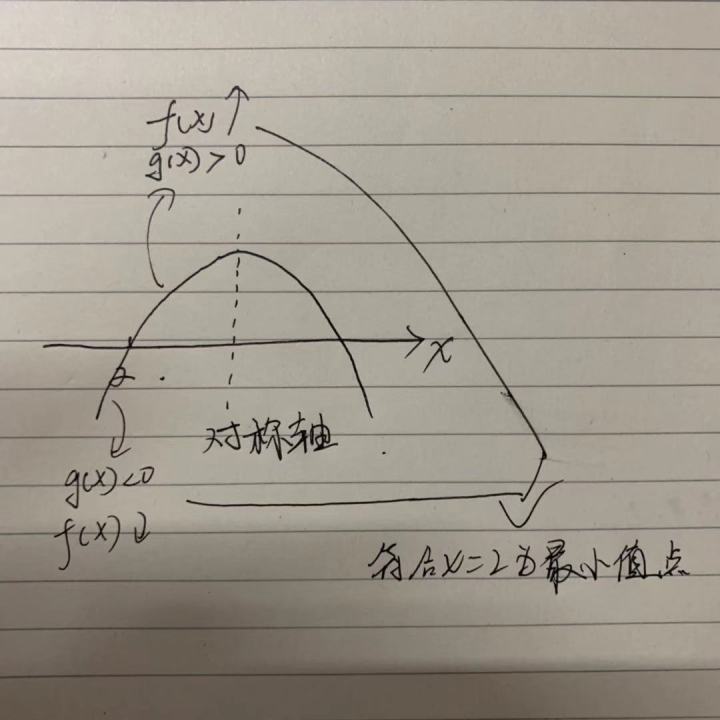
那么是不是可能有两种情况嘛,一是对称轴在x=2右边,二次函数开口向下;二是对称轴在x=2左边,二次函数开口向上。
Ⅱ. a<0且 ,无解;
Ⅲ. a>0且 ,此时
.
最后回想,这个题我还有什么地方没有写到吗,回想我们的整个逻辑,嗯,完整,OK。
那么综上,.
(北京卷13分的导数题我们就这样拿到手了)
欢迎关注我们的连载,学习数学三招的思维

