本质教育高考数学破题解析开课啦!!!
每周一、三、五更新新篇,将会从18年高考开始,致力于用三招将高考数学中具有代表性的题逐个击破。
本质教育高中数学致力于培养学生的思维方式,提供思维能力,打破固有的刷题和死记硬背模式,让学生冲刺高考数学的140+。
本质教育高中数学网址:本质教育高中数学
数学三招:翻译、特殊化、盯住目标
翻译:文字、数学语言、图形,将题目中出现的这三者进行合理的相互间转化。
特殊化:根据题目或者选项的限制条件,取一些特殊值或特殊的式子,寻找特殊规律,再推及一般规律,在高难度的题中可以用特殊化进行猜想。
盯住目标:紧盯目标,联想相关的定理、性质、公式,与题目已知联系起来,进行解题,在难题中有时候也可以用盯住目标联想公式进行合理猜想。
三招虽然简单易懂,但是如果要熟练运用,难度还是很大的,所以,也就有了我们本质教育高中数学。
2018.8.22更新
(过于简单的题目不再赘述,这里我们只选取稍微凸显思考的题)
2018年全国Ⅰ卷理科数学(大题部分)
试卷第17题
在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;
(2)若DC= ,求BC
三招破题
(1)盯住目标:求cos值,则我们需要把图形翻译出来,然后找到所求的角,根据学过的知识求解即可。
翻译:根据条件我们可以画出图如下:
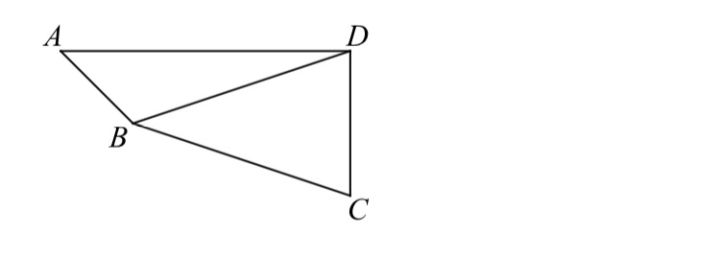
那回到我们的目标,我们求一个角的余弦值,联想定义和性质,发现我们构建三角形,根据三角形定义求解会更简单。
可以作BM⊥AD,交AD于M,那么显然AM=BM= ,
根据勾股定理,BD=5,那么DM= ,
则 cos∠ADB=
(2)盯住目标:求BC边长,题目中知道CD和BD,那联想学过的l定理是不是就是余弦定理,那是不是还需要∠BDC,而BDC又与ADB互余,则我们是不是可以通过ADB的正余弦求出BDC的正余弦,则应用余弦定理即可。
cos∠BDC=sin∠ADB=
CDB中,由余弦定理:
代入数据即可得到BC=5。
(不需要背套路,不需要日复一日的题海,盯住目标和掌握基本定义的翻译即可解题)
欢迎关注我们的连载,学习数学三招的思维
需要试听课程请添加客服老师微信(微信号:ZGSX02)咨询

